The End Of Knowledge - Vault 5/80 - CVPR - 2022 - Shape Learning in Biomedical Imaging

graph LR classDef shape fill:#f9d4d4, font-weight:bold, font-size:14px classDef learning fill:#d4f9d4, font-weight:bold, font-size:14px classDef manifolds fill:#d4d4f9, font-weight:bold, font-size:14px classDef applications fill:#f9f9d4, font-weight:bold, font-size:14px classDef geomstats fill:#f9d4f9, font-weight:bold, font-size:14px A[Shape Learning in
Biomedical Imaging] --> B[Shape learning:
machine learning on shapes 1] A --> C[Biomedical imaging:
biological structures, various scales 2] C --> D[Shape-biology link:
structure, function, health 3] C --> E[Imaging techniques:
MRI, microscopy, cryo-EM 4] C --> F[Biomedical questions:
shape changes, disease 5] C --> G[Shape reconstruction:
extraction from images 6] B --> H[Shape modeling/representation:
numerical representation for analysis 7] A --> I[Manifolds: curved
generalizations of vector spaces 8] I --> J[Shapes as manifolds:
object surface 9] I --> K[Shape spaces as manifolds:
all possible shapes 10] I --> L[Shape transformation spaces
as manifolds: motions, deformations 11] B --> M[Statistics generalized
to manifolds 12] M --> N[Manifold geometry:
inductive bias for learning 13] B --> O[ML problems on manifolds:
supervised, unsupervised, RL, optimization 14] O --> P[Manifold learning building blocks:
points, tangents, geodesics, distances 15] O --> Q[Vector space to
manifold ML conversion 16] A --> R[Geomstats: Python package
for manifold computations 17] R --> S[Learning on Riemannian manifolds 18] R --> T[Pose/transformation manifolds: SE3 19] R --> U[Manifold taxonomy:
abstract to concrete 20] B --> V[Manifold-adapted ML overview 21] V --> W[Dimension reduction on manifolds:
PCA, autoencoders 22] W --> X[Geometric view:
principal subspaces 23] V --> Y[Variational autoencoders VAEs 24] Y --> Z[Generalizing VAEs to manifolds 25] Z --> AA[mVAE components:
exponential map, geodesic distance 26] Z --> AB[mVAE vs alternatives:
faster than MCMC 27] Z --> AC[mVAE explains
VAE latent space curvature 28] A --> AD[Shape analysis pipeline:
extraction, modeling, manifolds, insights 29] A --> AE[Ongoing research:
generalize ML, biomedical applications 30] class A,H,M,N,V,W,X,Y,Z,AA,AB,AC learning class B,D,F,G,J shape class C,E applications class I,K,L,O,P,Q,S,T,U manifolds class R geomstats

Resume:

1.- Shape learning: Machine learning on data that are shapes, with each data point being one shape.

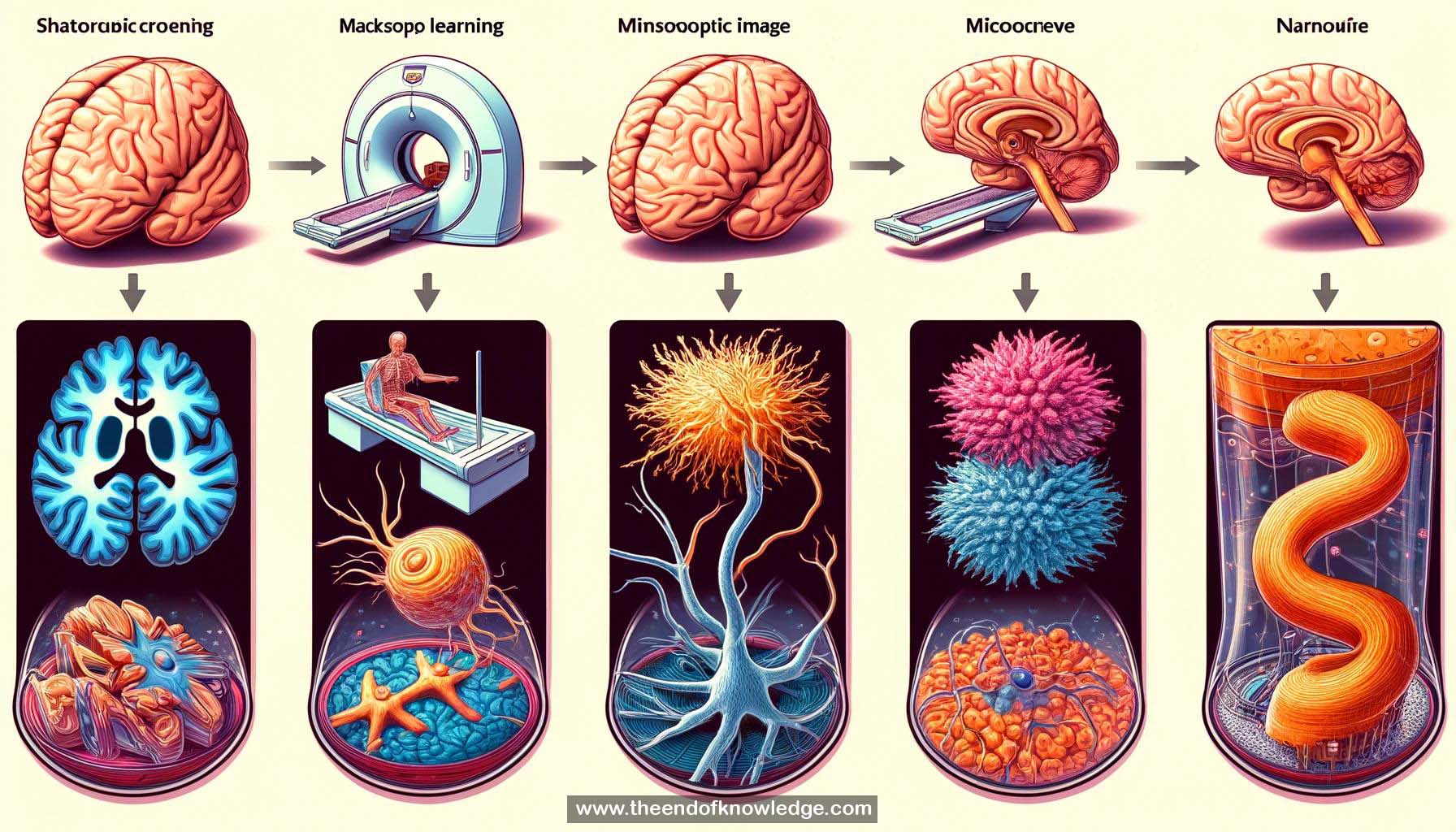
2.- Biomedical imaging: Studying biological structures through imaging techniques at various scales (organs to molecules).

3.- Shape and biology link: A biological structure's shape is linked to its function and health/disease state.

4.- Imaging techniques: MRI, microscopy, cryo-electron microscopy enable observing biological shapes at different scales.

5.- Biomedical questions: Research aims to answer questions about biological shape changes, e.g. brain atrophy in Alzheimer's.

6.- Shape reconstruction: Extracting shapes from images through algorithms like segmentation before analysis.

7.- Shape modeling/representation: Representing extracted shapes numerically in a computer for analysis.

8.- Manifolds: Generalizations of vector spaces that can be curved. Many shape representations give rise to manifolds.

9.- Shapes as manifolds: A shape itself can be a manifold (e.g. surface of an object).

10.- Shape spaces as manifolds: The space of all possible shapes of a certain type forms a manifold.

11.- Spaces of shape transformations as manifolds: Sets of shape motions or deformations can be modeled as manifolds.

12.- Generalizing statistics to manifolds: Traditional statistics don't apply on manifolds. Statistics must be generalized.

13.- Manifold geometry as inductive bias: Incorporating knowledge of shape space geometry can improve machine learning algorithms.

14.- Types of machine learning problems: Supervised, unsupervised, reinforcement learning, optimization - all can be generalized to manifolds.

15.- Manifold learning building blocks: Points, tangent vectors, geodesics, distances, exponential map - used to translate ML to manifolds.

16.- Vector space to manifold conversion: Translating ML building blocks allows converting many algorithms to manifolds.

17.- Geomstats package: Open-source Python package implementing manifold computations for manifold/geometric learning.

18.- Learning on Riemannian manifolds: Package supports various algorithms on Riemannian (metrizable) manifolds.

19.- Pose/transformation manifolds: Example manifold is SE(3) - the space of 3D rotations and translations.

20.- Numerical taxonomy of manifolds: Hierarchy/taxonomy of manifolds from abstract to concrete, implemented in geomstats.

21.- Manifold-adapted ML overview: Research aims to generalize ML algorithms across different manifolds.

22.- Dimension reduction on manifolds: Generalizing linear (PCA) and nonlinear (autoencoders) dim reduction techniques to manifolds.

23.- Geometric view of dim reduction: Finding principal subspaces within linear spaces or manifolds.

24.- Variational autoencoders (VAEs): Learn nonlinear latent subspace of data space assuming generative model.

25.- Generalizing VAEs to manifolds: Adapting VAE components (generative model, loss function) to manifold versions.

26.- Manifold VAE (mVAE) components: Exponential map replaces addition. Geodesic distance replaces Euclidean. Loss functions adapted.

27.- mVAE vs alternatives: mVAE faster than MCMC-based manifold dim reduction method.

28.- mVAE explains VAE latent space curvature: Manifold perspective shows why VAEs tend to learn flatter latent spaces.

29.- Overall shape analysis pipeline: Shape extraction, modeling, computing on manifolds, generating insights.

30.- Ongoing research: Further generalizing ML to manifolds, applying to biomedical shape data.

Knowledge Vault built byDavid Vivancos 2024